David McNaughton: Islamic Astronomy Correspondence

A.
(i) Whenever there is a three-day difference between their respective Ramadan dates. This was indeed the case in 1412 H (March 1992) - but only in the Far East and in parts of India; (in Pakistan the difference was only two days). The Saudi Arabian and Bohra dates were actually identical that year - but only because of the calendar system being used by the Saudis at that time. However, the Bohra 1st Ramadan 1519 on 26 December 2095 will certainly be three days earlier than is possible by moonsighting. Also, the Bohra 1st Dhu al-Qa'dah 1434 on 5 September 2013 will be three days too early.

(ii) Whenever the old crescent is prominent in the early morning sky just as the Bohras start their fasting. This came close to happening on 29 December 1997. Other dates to watch in the future are 31 May 2212, 20 January 2387, 18 June 2471, 2 May 2736 and 9 July 2860.

2.
C. From Awny Al-Omari, Wisconsin, USA, January 1996:

I think I have found another 'hole' in the Ahmadiyya theory of double eclipses. It seems impossible to have eclipses on the 13th and 28th of the same Islamic month, as they claim. The gap between them cannot really be that great, can it? - remembering that the lunar one must take place at night and the solar one during the day?

R.
The interval between Full Moon (for a lunar eclipse) and New Moon (for a solar one) averages just over 14.75 days, but may take on quite a range of values - between 13.9 and 15.6 days. The interval between the two Ahmadi eclipses (21 March to 6 April 1894) was just over 15.5 days - but there was nothing abnormal or extraordinary about that. The distribution of possible values is not unimodal. Instead, it is markedly saddle-shaped, such that we are more likely to get an interval-length around 15.5 days (or else about 14 days) - than a value near the 14.765-day mean. This is illustrated in the histogram below (constructed for AD 1600 to 2400 by Ala'a Jawad of Kuwait, and printed in Sky & Telescope November 1993, page 77):

Copyright © 1993 by Sky Publishing Corporation - used with permission.

The longest intervals straddle a lunar apogee, whereas the short ones contain a perigee. Alternation between the two extremes follows a 412-day cycle. (Item 5 depicts another feature of this same rhythm).

[Also see question 15].

3.
Q. From Mr S.V. Ali, UAE, 22 January 1999:

Is it possible to prepare an Islamic calendar in advance, after predicting lunar sightability using modern technology? It would be better if Muslims all over the world could celebrate Ramadan and Eid on the same day, if possible.

A.
Calculations can sometimes predict that the crescent definitely will (or will not) become visible. However, they cannot always do that because of daily and local fluctuations in atmospheric water vapour and dust content. Often we have to resort to expressions such as "unlikely at sea-level" or "probable in mountain regions".

If people are happy to base a predetermined Islamic calendar on purely mathematical guidelines - as the Bohra community already does - then there is a wide choice of criteria. For example, you could refer to the age of the New Moon in hours, or to the time-lag between sunset and moonset, or (best of all) to the number of degrees separating them at dusk (see article on calendars). The rules must be rigidly and precisely defined to avoid ambiguity and dispute. Such dates will often correspond with the first appearance of the crescent, but there will of course be exceptions.

Inevitably, there will then be occasions when the moon does not quite attain the prescribed threshold, and others when it only just surpasses it. In rare instances, extremely accurate computations will be necessary to decide whether or not a borderline date qualifies. Thus, the defining criteria must also specify the observer's exact location.

Sighting always becomes easier as you move west, because the local time of sunset becomes later - when expressed in Universal Time. And each extra hour of "delay" in the sighting-time - enables the moon-sun separation to increase by another half-degree.

Also, the crescent will sometimes be more easily visible in the opposite hemisphere, because of seasonal variations in the angle between the horizon and the sun-moon line.

If people wish to devise an Islamic calendar applicable to the entire globe, then there are limited options - for example:

a) Calculations of solar and lunar heights - or setting times, or whatever - may be made for a universally accepted location - perhaps Mecca.

b) Alternatively, the decision can be based (indirectly) on the time of birth of New Moon, which can be forecast with an accuracy of one or two seconds. That is the instant when the moon crosses the line between the Earth and sun, so it is the same for every country.
- - - - - - -

Adapted from my reply to Muhammad Hafiz of Guyana, 19 August 2000:

(i) Mathematical techniques can predict accurate celestial positions for the sun and moon for the next few centuries - but only in 'Dynamical Time' - see (ii) below. (The long-term deceleration of the moon in its orbit constitutes the biggest uncertainty in this context - but that becomes significant only if we are trying to look a thousand years or more ahead).

(ii) We also need to examine moon-sun relationships as viewed from specific terrestrial locations - and at times which are defined locally (such as sunset and moonset). And to do this properly, we are compelled to keep track of changes in Earth's rotation-rate. Unfortunately, these can be quite irregular - such that nobody knows exactly how they will behave in future. This means that we are unable to forecast, many decades in advance, high-precision sunset minus moonset intervals at Mecca, say. If we are looking only a few years ahead, however, then this problem is not too critical. (Nevertheless, this is why astronomers maintain two completely separate scales - namely Universal Time, which is constantly readjusted whenever our planet undergoes a 'convulsion' - and Dynamical (or Atomic) Time, which is quite smooth but less useful for civil purposes).
Celestial coordinates, such as Right Ascension and Declination, are independent of Earth's orientation - so those coordinates can easily be measured in Dynamical Time.

(iii) Whether a new-born crescent either will, or will not be spotted - depends very much on atmospheric visibility. Success also depends on quality of eyesight of an individual observer. The 'grey area' extends through several degrees of altitude.

(iv) Unfortunately, day to day variations in air cleanliness cannot be foreseen more than a week or so in advance (and even that is optimistic). Thus, any mathematically based model which outputs crescent sightability - should be regarded only as a rough guide. No modern-day algorithm is capable of infallible lunar prognoses on every occasion.

(v) There is nothing wrong (on purely scientific grounds*®) with a particular community adopting a mathematical model to construct a personal lunar calendar. But in this context, it is not helpful to be presented with answers qualified by 'possibly', or 'fair chance', because a clear-cut 'yes/no' decision has to be taken. Thus, a sharply defined arithmetic threshold must be chosen; astronomers then need to determine if the crescent has passed over it, or whether it has not. There must be no intermediate grey band of uncertainty whatsoever, in such an exercise. But there is no easy way of deciding which of several alternative models is best.

¬*If, on the other hand, there are religious objections to utilising mathematical rules for constructing a lunar calendar, then that is of course a completely different matter.
- David McNaughton

[Also see item 19].

4.
C. (From Abdul Karim ChalermThai, UAE, 6 April 1999):

It is somewhat disconcerting to notice Dr Ilyas writing about "absurdly differing dates" and "chaotic conditions" with calendars used throughout the Islamic world.

R.
Yes, there is confusion because Saudi Arabia and the other GCC countries tend to commence Ramadan between one and three days earlier than most other countries. At the beginning of every year up until 1419 H, the Saudis used to prepare a "reference" calendar based on a 10631-day cycle, and were extremely reluctant to depart from its dates. Often, the Saudi calendar was identical to the Bohra one. That was the reason why there were four different Ramadans in 1412 H, starting on (the mornings of) 4th, 5th, 6th and 7th March 1992 respectively! In the Saudi calendar, there used to be strict alternation between 29-day and 30-day months (except at the end of "leap" years) - but that was certainly not how the moon behaved. For 1420 H the Saudis have modified their pattern slightly, but there will still be disagreements with the rest of the world. If you wish, examine the criteria adopted by Saudi Arabia at times in the past and at present.

5.
C. From Khalid Shaukat, USA, 23 June 1999:

Lunation-cycles are certainly interesting and intriguing, but they do not really have much relevance to the problem of crescent visibility and Islamic calendars, do they?

R.
It is always worth mentioning the variations in lunar migration-rate, when answering people who like to quote the age of the moon as a guide to sightability. And by illustrating those variations in terms of clearly defined cycles, we demonstrate that the dynamics and the astronomical principles are well understood.

More important than the age is the question "How much physical separation is there between the sun and moon?" - and that can vary quite significantly. During a 17-hour period, for example, sometimes a new-born moon moves little more than 8 degrees through the stellar background. On other occasions, it can migrate almost 11 degrees in 17 hours. And those extreme values could well result in a failure - or a success, respectively.

Those fluctuations in the speed with which a New Moon is moving away from the sun, vary according to how close the New Moon is to perigee or apogee. Furthermore, a New Moon/perigee coincidence tends to recur every 14 lunations, which is almost the same as 15 anomalistic months. (An anomalistic month is the time-interval between successive perigees).

Here is an illustration of that 14-lunar-month cycle:

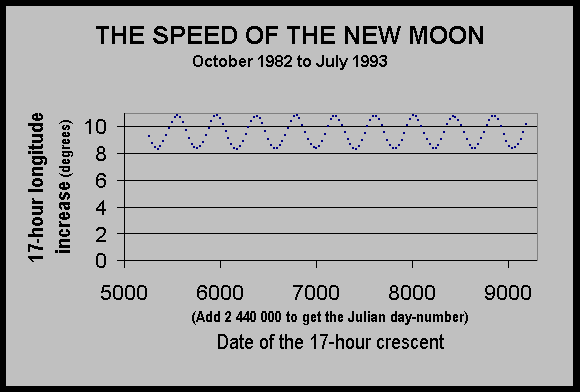
On a long-term basis, the cycle in lunar month-length averages 411.78 days - which is actually slightly less than 14 lunar months. This difference involves further small adjustments - but that is another story.

Another occasion when it is worth describing the fluctuations in the lunar orbit - is when three or four consecutive 30-day months are recorded - and someone asks how that can be possible. It often happens near the peak of the 412-day cycle, particularly when it synchronises with the 9-year cycle in month-length.

6.
Q. From Khalid Shaukat, USA, 24 June 1999:

Please give a specific example of five successive 30-day months.

A.
Calculate the likelihood of crescent visibility on 17 November 2009 and again on 15 April 2010 - at the two following locations:

(i) 28 South latitude, 0 longitude (i.e. on the Greenwich meridian) - and (ii) 28 South latitude, 15 West longitude.

The moon will be visible on the first date, but not on the second. The next month will therefore commence (at dusk) on 16 April 2010 - exactly 150 days after the start of the first month (which was at dusk on 17 November 2009).

An important feature of this example is that the moon's latitude changes from negative to positive during those five months. Its positive latitude reduces its altitude above the horizon in April 2010: that makes it much harder to spot it. (Remember that the southern sky is "upside down").

The fact that the chosen points are at sea rather than over land - is not important because we are examining only the theoretical possibility of five consecutive long months. This phenomenon could therefore occur anywhere on latitude 28 South.

It is much more likely to happen in the southern than in the northern hemisphere, for various astronomical, geographical, trigonometric and geometric reasons. Thus, the chance of experiencing five successive 30-day months will increase if you go even further south. Admittedly, it is quite rare even in southern latitudes.

Incidentally, if the above illustration does not work with your own personal crescent-sighting criteria, then move slightly east or west on the same latitude, and rerun your calculations there.

7.
C. From Nasreen Hasan, Canada, 5 July 1999:

You say that the shape of the lunar orbit repeats itself every seven lunar months. Thus, according to Kepler's Laws of Celestial Motion, the time taken for the moon to orbit the Earth - should also repeat itself every seven lunar months. I am puzzled as to why 14 lunar months should be required for a complete cycle in month-length.

R.
Although the dimensions of the lunar orbit are repeated approximately every seven lunar months, the moon is not following a perfect ellipse in its orbit, so Kepler's Laws cannot be applied exactly. The moon's movement is constantly being disturbed by the pull of the sun. During the course of seven lunations, the sun's position switches from the perigee to the apogee end of the moon's orbit, so its modifying effects on the moon's movements will inevitably change too. For example, the moon's path always curves comparatively sharply at a Full Moon perigee because Earth and sun are pulling in the same direction. However, that curvature is less at a New Moon perigee - consistent with the laws of dynamics.

Complex behaviour is also implied by the saddle-shape of the histogram accompanying answer 2 above.

By halving the quantities discussed in answer 5, you will see that the 7-lunation cycle in eccentricity is almost equal to 7½ anomalistic months (206 days). There is even a third type of "month" which helps to illustrate changes in the moon's behaviour; it involves calculating the "instantaneous eccentricity" in the lunar orbit. We then find that there are 31.8 days between successive maxima or minima, so 13 of these "eccentricity months" are very nearly equal to 14 lunar months (and to 15 anomalistic months). This 412-day period is therefore the time taken for everything to become synchronised again.

The following diagram is Figure 1a from Jean Meeus's book Mathematical Astronomy Morsels, published in 1997 by Willmann-Bell. It shows how the 31.8-day cycle interacts with the 206-day cycle in eccentricity (whose values are given along the y-axis):

A lunar double-cycle
Instantaneous
eccentricity

Copyright © 1997 by Willmann-Bell, Inc. - used with permission.

8.
Q. From Fatma Kazim, UAE, 1 December 1999:

If we note down the day of the week when the 4th of Rajab occurred, then can we assume that the 1st of Ramadan will fall on the same weekday?

A.
That rule will work only if Rajab and Sha'ban together straddle 59 days; i.e. if one of them contains 30 days while the other lasts 29 days. That does indeed happen on the majority of occasions.

However, it is not at all uncommon for both of them to be 30 days long - or they can both be 29-day months. In these latter two instances, your rule will break down.

9.
Q. From Rashid Abdulkareem, Ohio, USA, 6 December 1999:

What are the physical reasons preventing the New Moon from being spotted during (say) the first six to ten hours after its 'birth'?

A.
Two factors make an extremely young crescent difficult or impossible to be seen:

a) Because it is very close to the bright glare of the sun, and

b) Because it is extremely thin (just like a line, in fact).

As the crescent gets older, it moves further away from the sun, and therefore into a part of the sky where the solar glare is not quite so bright. At the same time, the crescent becomes wider (thicker) as it ages.

There is no sudden change between being invisible - and becoming visible. A lot depends on how clear and how thick the air is. As you ascend through the atmosphere, the air becomes less dense and cooler, and therefore holds smaller quantities of dust and water vapour - making it easier to see a new-born crescent. Also, there is considerable variation in the quality of people's eyesight.

Incidentally, even a good telescope may be 'blinded' by the solar glare, and is only slightly better than the unaided eye for seeing an extremely young crescent.

10.
Q. From Rashid Abdulkareem, Ohio, USA, 7 December 1999:

What could help us decide whether reports of crescent-sightings are genuine or not?

A.
Observers should be required to give the exact time and if possible the compass direction of their sighting. If no compass is available, they should refer to the point on the horizon where the sun had set. It would help too (when they see the New Moon) if they could estimate its height above the horizon (remembering that two lunar diameters equal one degree - or else use other methods of measurement). They should be asked whether the crescent was 'flat', or tilted to the left or to the right. Lastly, if there were any bright stars or planets nearby at the time, then their positions should be noted and described - and preferably drawn accurately on a diagram.

All those above-mentioned facts and attributes may be verified using suitable programs. These computer calculations are reliable. Confidence in them is enhanced by examining where they position the crescent on the second and third days after its birth - when the moon and other celestial objects become very easy to identify later in the evening.

In addition, exact times of New Moon birth can be measured using laser-beam reflectors placed on the moon by astronauts: they compare very well with the computer predictions. Remember too that forecasts of solar and lunar eclipses, and of lunar occultations of stars and planets (and solar transits) - always correspond precisely with what observers see later.

See also question 12.

11.
C. From Raza Jaffri, UAE, 12 December 1999:

The shortest day in the year is supposed to be on 21 or 22 December, but this does not seem to be reflected by the Iftar and Imsak times published for Ramadan 1420 here in Dubai, UAE. I am also puzzled because Imsak continues to become later every day - even after 22 December. It looks as if they have made a mistake?

R.
(i) For practical reasons, published times of Imsak and Iftar are usually rounded off to the nearest minute. Subtracting them therefore gives only a very rough idea of the length of your days.

(ii) Precise identification of the shortest day in the year at your latitude - requires calculations accurate to the nearest second or two. This is a warning against deducing too much from figures which have been corrected to the nearest minute. And at this level of accuracy, the use of Imsak instead of sunrise could well give a different indication as to which really is the shortest day - because Imsak occurs about 80 minutes before sunrise. (In other words, you would also need to consider how that 80-minute interval varies during December).

(iii) In any case, meteorological fluctuations in temperature and pressure can easily induce extra changes of 20 seconds or more in Imsak and in sunrise/set times.

(iv) It is not really feasible to query the official times for Imsak and Iftar - without knowing (in precise detail) what astronomical criteria were used to compute them - and exactly what location they apply to (within a few kilometres, if possible).

(v) The date of latest sunrise does not occur on the shortest day of the year. In the Arabian/Persian Gulf, it takes place in or just before mid-January. Two factors contribute to this 'irregularity'. The easiest one to understand is the variation in Earth's speed during its orbit round the sun. Often, this displaces the sun away from what can be called its 'normal' or 'mean' position. Thus, during January astronomers say that the sun is several minutes 'behind schedule'. This makes sunrise (and sunset) times later than would be expected if Earth's orbit was a perfect circle. See the more detailed explanations in this website and outside.

12.
Q. From Muhammad Ridha Shushtary, Teheran, Iran, 13 January 2000:

If no crescent is seen on 30th Shawwal, then did Ramadan finish too early?

A.
Almost always, because a 30-day period invariably embraces one complete lunar circuit plus a few extra hours. And during that extra time, the New Moon moves further away from the sun. Thus, if you wait the full 30 days after a successful sighting, then the next month's moon should be even more obvious.

An exception to the rule could occur when the lunation (or circuit-time) is close to 29 days 20 hours, and the month commenced after a sighting (in extremely clear conditions) with just nine degrees of celestial longitude separating the sun and moon. For the following New Moon, the 'four extra hours' would increase that longitude difference to only 11 degrees - which still places the crescent in the 'grey' area of marginal visibility, where success depends on the amount of water vapour and dust in the air. (Of course, after widening our observation-base, we could certainly regard that second crescent as 'sightable from somewhere in the region concerned').

After only 29 days, incidentally, a new-born crescent is more difficult to identify than the one seen at the start of the previous month (assuming clear weather on both occasions).

13.
C. From Mahmood Essa, Mombasa, Kenya, 16 January 2000:

I am having difficulty picturing the process whereby a New Moon can try to 'overtake' the sun while they are both setting (on 6 January and 5 February 2000, for example).

R.
There may be some confusion between what may be termed 'the moon's slow migration' - and its 'setting', i.e. its descent towards the horizon.

The setting of the sun and moon are caused by the Earth's comparatively rapid spin. In the evening, this makes them appear to move downwards in the western sky at about 15 degrees per hour (in your latitudes).

However, the slow migration of the moon and sun are in the opposite direction - namely upwards when they are in our western sky. To picture that, forget about Earth's spin for a moment. Imagine the moon and sun attached to the inside surface of a gigantic planetarium representing the firmament - showing us where these heavenly objects are in relation to the stars. (The stars are always there in the sky, but during the day they are hidden by the solar glare).

In relation to the starry background, the sun creeps along at about one degree per day, while the moon migrates at 13 degrees per day (on average, see answer 5). That means that the moon catches up with (and eventually overtakes) the sun at a speed of 12 degrees per day. To watch this happening properly, you would need to leave the spinning Earth and suspend yourself in space (whilst remaining near Earth). Nevertheless, even here on the ground, you can often notice the moon's slow migration during the course of an hour or two - if there happens to be a bright planet or star nearby.

The slow upward migration of the New Moon away from the sun - results from the moon orbiting round the Earth. (The sun's apparent migration through the firmament is produced by Earth orbiting round the sun).

Notice that 30 days multiplied by 12 degrees gives 360 degrees - which makes sense, because that takes the moon right round the firmament in one month - bringing it back level with the sun again.

14.
Q. From Mohammad Odeh [of ICOP and the Jordanian Astronomical Society], Amman, 7 May 2000:

Some people want to base the end of Ramadan on crescent-sighting, and then to use calculations (e.g. comparing moonset with sunset) for the start of Dhu al-Hijjah. But my own research shows that sudden changes in criteria have sometimes produced 28-day and 31-day Islamic months in Jordan. For example, our Sha'ban 1412 in March 1992 finished after just 28 days.

Saudi Arabia now seems to be improving its calendar rules, compared with the system which it followed in 1412 H. But is it possible that their new criterion (moonset to be later than sunset at Mecca) will also yield 28-day months - if they use it to start Dhu al-Hijjah following an Eid al-Fitr which was decided strictly by crescent visibility? Is it feasible to demonstrate this with a specific example?

A.
Yes, that could quite easily happen in 1439 H. Many countries (like Pakistan and Malaysia) will almost certainly wait till the evening of 15 June 2018 before commencing their Shawwal 1439. It is true that the crescent might just be visible at Mecca on the previous evening (14 June) if the sky is exceptionally clean and free from dust-haze, but it will be quite difficult. At Mecca on the 14th, I calculate the vertical separation between the centre of the setting sun and the base of the crescent to be less than nine degrees, allowing for parallax. That value is not normally enough to ensure success.

Now come to 11 August 2018 for the beginning of Dhu al-Hijjah 1439, and apply the new Saudi rule. Moonset is definitely after sunset that day at Mecca (and indeed at Calcutta and in some places further east), although the crescent will certainly not be seen in Asia that evening. So, under the revised Saudi system, the new month will commence. But this is only 57 days after 1st Shawwal (assuming that waits till the evening of 15 June), in which case either Shawwal or Dhu al-Qadah will have to be cut to 28 days.

To prove beyond doubt that the 28-day anomaly is theoretically sometimes possible, we can rerun the Eid al-Fitr calculations for 110 degrees East on the same latitude as Mecca. At this place (near Calcutta and Dhaka), the moon-sun vertical separation on 14 June will be less than seven degrees - so a 'sighting' there will be extremely unlikely. If necessary, we could of course move even further east for illustration purposes.

I maintain that this recalculation for a place further east is a valid demonstration that the 28-day anomaly will occasionally take place at Mecca. In addition, lunar latitude on the evening 14 June 2018 is only minus 2.67 degrees, but it can sometimes decrease to almost twice that value. And with maximum negative latitude, a Mecca sighting on 14 June 2018 would move into the 'rather unlikely' category.

This 28-day anomaly is due to the fact that lunar circuit-times during Shawwal and Dhu al-Qadah 1439 are significantly shorter than normal - not far above their minimum possible value, in fact.

15.
Q. From Awny Al-Omari, Wisconsin, USA, 25 January 1996:

If the Ahmadiyyas maintain that a solar eclipse can sometimes occur on the 27th of a lunar month, then presumably a lunar one should be feasible on the 12th? However, they regard the 13th as the earliest possible day.

A.
It is actually difficult to see how a solar eclipse could be witnessed as early as the 27th (see separate file). A sighting at dusk next day would terminate the month incorrectly after just 28 days. Of course they could postulate hazy conditions at the beginning and end of the Islamic month - thereby delaying the identification of the crescent (at a location specifically selected for their purpose).

Indeed, atmospheric visibility is one of the parameters they are prepared to vary, when it suits them. In particular, they need to assume that the Ramadan crescent was not seen from Qadian (near Lahore) on 8th March 1894. Only by postponing the start of the Holy Month, were they able to regard the date of the lunar eclipse as 13th Ramadan. However, it is likely that the New Moon would have been spotted on 8th March from places at higher altitude to the north or east, where the air was thinner, cleaner and drier.

Naturally, the Ahmadiyyas do need to be consistent with their criteria. And with the right combination of circumstances, there will then be situations which result in lunar eclipses occurring even earlier - on the 12th of an Islamic month.

This will happen at locations
(i) where thick haze delays the beginning of the month by an extra day or two,
(ii) where the inclination of the ecliptic is unfavourable for moonsighting, and
(iii) whenever the interval between New and Full Moon is less than 14 days; (this is not at all uncommon: see the histogram in question 2 above).

For example, poor atmospheric visibility would also have obscured the Ramadan crescent on 8th March 1894 at latitude 40 South, longitude 120 West. If based on observations made just at that point, the new month would then have had to wait till the evening of the 9th. And the subsequent lunar eclipse on 21st March would have been in the early hours of the morning - which at that particular place was still the 12th of Ramadan.

So as you suggest, the 12th (not the 13th) is the first date when lunar eclipses can be witnessed (using criteria which the Qadianis themselves have adopted - but which can cause problems - see question 16). Thus, their March 1894 lunar eclipse did not occur on the earliest day possible. [See item 18 in this file].

Also refer to the article at http://www.dlmcn.com/qadfl.html

CALCULATIONS & REFERENCES

At dusk on 8th March 1894 at 40º South, 120º West, the base of the crescent was only 7.2º above the centre of the sun (ignoring refraction but allowing for parallax). Azimuth difference was 16.3º.

There are well-documented cases where the moon was not visible under similar circumstances:

"Visibility of the lunar crescent" by B.E. Schaefer (1988). Q.J.R. Astron. Soc., 29, 511-523. (See observations 16, 22, 28, 99 and 100 in his Table I).

"Lunar crescent visibility" by B.E. Schaefer (1996). Q.J.R. Astron. Soc., 37, 759-768. (See his Figure 3).

"Limiting altitude separation in the New Moon's first visibility criterion" by M. Ilyas (1988). Astron. Astropys. 206, 133-135. (See his Figures 1, 2, 3 and 5).

However, if someone feels that the New Moon would probably have been visible on 8th March 1894 at 40º South, 120º West (even in hazy conditions), then we could recalculate for an observation point slightly further poleward - say at 45º South, 120º West - where it will be much harder to spot the crescent.

In addition, lunar latitude on 8th March 1894 was only -0.3º, so it could easily have been more unfavourable. For instance, on 8th February 2008, lunar latitude will be almost +1.0º, and at the beginning of nautical twilight (at 42º South, 50º East, say) the crescent will be extremely close to the horizon - impossible to see even in moderate haze. A locally determined new month at that particular place will have to wait till the evening of 9th February. Thus, the subsequent lunar eclipse on 21st February 2008 will be observed there (before dawn) on the 12th of the month.

October 1986 provides a similar illustration, this time from the northern hemisphere.

16.
C. From Sheeba Mumtaz, Australia, 14th May 2000:

In our local community, some people insist that the Ramadan and Eid crescents should always be sighted from here, not from elsewhere. When the sky is hazy (or perhaps even cloudy) on the 29th of the month, that obviously means continuing it to a 30th day. Other people believe that we should be prepared to telephone elsewhere, but opinions vary as to what distance is acceptable.

R.
Suppose the beginning of Ramadan is postponed at a location where thick dust-haze obscures what would otherwise be an obvious crescent. There is then a definite possibility that the air will become quite clear for the Eid sighting. If that particular Ramadan would normally have lasted only 29 days, then the delay in its start - will result in an unacceptable end after just 28 days.

Remember that two or even three successive 29-day months do sometimes occur naturally.

An example is provided by 13th June followed by 12th July 1991 at 25ºS 65ºE. The crescent could have been disguised by local haze on that first date, when the sun-moon configuration resembled records 273 and maybe 262 of Schaefer, 1996 (referenced in my answer 15 above); see his Table I. Extending the earlier month into a 30th day (thus ending it at dusk on 14th June 1991) would have cut the subsequent month to 28 days upon a sighting on 12th July - which was certainly feasible there in clear conditions. (If desired, different criteria for success or failure may be adopted - simply by moving the observation point several degrees, perhaps further east or south).

Admittedly, these are not Ramadan dates, but they demonstrate that the problem could easily occur during any Islamic month.

Incidentally, I deliberately chose an example where haze (not just cloud) could have obscured the crescent - because if the sky is overcast, people are more likely to inquire elsewhere. If the poor visibility is just due to haze, however, then it might be possible to miss the start of a new month without suspecting that there may be a problem.

My inclination and recommendation is to always consult observers in other towns - in fact even in other countries - provided you can receive the information in time to prepare your new schedule.

However, there is no 'perfect solution' to the Islamic calendar problem: see item 19.

17.
Q. From Mohammed Al-Bussaidi, Oman, January 2001:

Would it be feasible to launch an Earth-orbiting satellite to try and observe a new-born crescent, to decide when a new month should commence?

A.
I believe it would cause even more confusion. A lot will depend on the height and track of the proposed satellite, and also on which times and satellite positions will be deemed acceptable for its photography.

Bear in mind that the New Moon sometimes appears to pass more than five degrees 'above' or 'below' the sun. Under those circumstances, the satellite should be able to 'see' the crescent at the very instant of its birth, and indeed just before. Thus, there would be no way of distinguishing the old crescent from the new one in its photographs.

In addition, the parallax effect associated with space-based observations - will be quite different from that experienced on the Earth's surface. During the course of a half-orbit, parallax will change the apparent moon-sun separation by two degrees (and by even more if the satellite is quite high above the ground).

18.
C1. From Saleh Alladin, retired Professor of Astronomy, Osmania University, Hyderabad, India, March 2006:

You (David McNaughton) are perhaps the first person to claim that it is possible to observe a lunar eclipse on the 12th of an Islamic month.

On page 344 of his book "Hujajal Kirana" (in Persian, published in 1271 H.), Nawab Siddeeq Hasan Khan says that according to astronomers, lunar eclipses take place only on the 13th, 14th and 15th. He also affirms that solar eclipses are possible on the 27th (as well as on the 28th and 29th). These dates therefore form part of the Ahmadi thesis, supporting Mirza Ghulam Ahmed's oath that he was the Mahdi.

R1.
Celestial dynamics has made substantial progress during the last 100 years, particularly with the advent of powerful electronic computers. The lunar orbit is therefore much better known, understood (and tracked) now, than was the case in past decades or centuries. Furthermore, the theoretical foundations have been greatly refined - incorporating (for example) Einstein's work on Relativity (subsequently confirmed experimentally), which demonstrates that the mass of an object, including the moon, is effectively modified according to its velocity. In addition, the distribution of mass within the moon and the Earth has been well researched and documented (yes, these factors too affect the lunar orbit). Simultaneous numerical integration of mutual gravitational attractions of all principal planets and their satellites is now feasible - even if it is a gigantic task, so difficult that only a very small handful of institutions in the world are capable of undertaking it. Their enormous computers and sophisticated software manage to forecast times of New and Full Moon within just one or two seconds - and their predictions are confirmed using laser reflectors left on the moon's surface by astronauts. With these facilities, nowadays we can easily and accurately examine eclipses and Islamic months in the past and in the future, as well as calculating lunations and calendric start-dates.

In question 15 above, and in my article at http://www.dlmcn.com/qadfl.html - I have given specific examples of eclipses on the 12th of an Islamic month.

C2. From Professor Saleh Alladin, 2007:

As you (David McNaughton) mention and illustrate in your Question 2, the interval between New and Full Moon is confined to values between about 13.9 and 15.6 days. Presumably the permitted time-lapse between a Full Moon and the subsequent New Moon is similarly restricted? Thus, if a lunar eclipse did ever occur on the 12th of an Islamic month, it would not then be possible to have a solar eclipse on the 28th of the same month - as required by the Hadeeth which we quote.

R2.
You are right - nowadays a 12th/28th eclipse-pair can never be witnessed. However - the size and shape of the lunar orbit varies from one millennium to the next. There will be years in the very far future when that circuit is noticeably more elongated (and indeed larger) than at present - i.e., there is a definite possibility that a Full to New Moon interval will then exceed 16 days occasionally.

Jean Meeus describes how the moon's orbital eccentricity can change. For example, look at chapters 1 to 3 in his "Mathematical Astronomy Morsels". Variations in Earth's orbital eccentricity also affect the Moon's behaviour; see in particular pages 30, 31 and 34 in chapter 4 of Meeus's "More Mathematical Astronomy Morsels".

Longer-term variations in the shape of the moon's orbit are illustrated in Meeus's "More ... Morsels", chapter 6 (see figures 6a and 6b); these are discussed and explained in his "Mathematical Astronomy Morsels III", chapter 1. (All Meeus's books are published by Willmann-Bell Inc., USA).

19.
C. To Mohammad Odeh [of ICOP and the Jordanian Astronomical Society], February 2006:

There does not appear to be a neat and easy "perfect solution" for the design of an Islamic Calendar. It seems that the following four criteria should all be satisfied, if possible:

(i) The new crescent must be positively identified by reliable observers;

(ii) Information has to be received in time to inform every Islamic community in the world - so as to enable people to perform their religious duties;

(iii) Places which are just a few kilometres apart should not really adopt different Islamic dates;

(iv) Months must be either 29 or 30 days long ... (never 28 or 31).

Because it does not always appear feasible to achieve 100 percent compliance between all those factors, there presumably has to be some compromise - i.e., a certain amount of 'stretching and bending' is necessary (of at least one of the above four requirements).

In fact, even dispensing with (ii) and (iii) might not solve the problem completely. Looking back at my item 16, there could occasionally be a clash between (i) and (iv) if the weather just happens to be unfavourable over the entire region which is likely to yield a successful sighting. A lot therefore depends on how extensive is the area from which New Moon identification is feasible - and where the observers are actually waiting.
- David McNaughton

R.
From Mohamed Odeh, ICOP, (now based in Abu Dhabi, UAE), 8th March 2006:

Yes, those are indeed the four factors we need to look at carefully, to try and 'balance' them as far as possible.

[Also see item 3].

20.
C. To the International Crescent Observation Project, July 2009:

Here is a suggested algorithm for designing an Islamic calendar:
When dusk commences at 0ºN 180ºW, the geocentric celestial separation between the New Moon and the Sun must exceed 12 degrees ... (or we could specify 10 degrees, if people prefer that). If a calculation shows that this will happen, then the new month should start all over the world with that particular evening - adopting the date prevailing on the eastern side of the International Date Line.

The "onset of dusk" could be defined as sunset, or (much better) as the instant when the centre of the sun is six degrees below the horizon [at that zero-latitude location on the Date Line] - ignoring refraction.

The Sun-Moon "separation" is of course determined by their celestial latitudes as well as by their longitudes; Brad Schaefer calls it the "Arc of Light". Because it is measured from a geocentric perspective, topocentric diurnal parallax is irrelevant.

The above criterion should be examined near the end of every Islamic month. If it is not fulfilled, wait another 24 hours and apply the test again.

That decision-process would enjoy these advantages:

(a) The rule is unambiguously defined, and the essential, basic concept is not all that difficult to understand and appreciate (although the actual computation-procedure does need to be rigorously laid down - using technical terms);

(b) The same date would apply over the entire globe;

(c) Islamic dates will be known a long time in advance - which is helpful when planning celebrations; [the biggest uncertainty involves future variations in the value of "Delta-T", but that will not usually pose a problem - unless we try looking ahead now into the 22nd century, perhaps];

(d) The decision is absolutely clear-cut: i.e., the calculation yields either a firm "Yes" or a firm "No", with no 'grey area' of uncertainty. In particular, it does not depend on a consideration of whether or not a particular moon-sighting report is genuine.
-------------------

In addition, that rule will completely satisfy items (ii), (iii) and (iv) in Question 19 above ....
... and with regard to item number (i), we can say that [with 12 degrees separation] the crescent will definitely be sightable from some place in the world on the critical date (even if occasionally it will be visible only from the central Pacific Ocean - near Western Samoa, say).

Nevertheless, I do appreciate the difficulty regarding the above-mentioned suggestion - namely, the fact that [according to the all-important Hadith attributed to the Prophet Muhammed, PBUH] it is essential that somebody reliable must positively identify the new crescent.
- David McNaughton

R.
From Usama Hasan, July 2009:

Thank you for the algorithm. Many Muslim jurists are actually moving away from an overly-literalist view of the hadith you mentioned; i.e. they maintain that it is not essential for the crescent to be seen every month, but enough for us to know that it is visible.

It is the same with our daily prayers: it is not necessary for someone to watch and confirm the sunset every day – it is sufficient just to look at a clock to check that the sun has set.

E-mail: DLMcN@yahoo.com

Link back to main index

Link back to Islamic Astronomy

Link to other astronomy topics

Link to History and Religion