Cultural Souls reflected in their Mathematics:
the Spenglerian Interpretation
David L. McNaughton - DLMcN@yahoo.com
Centro de Educación Permanente "Blas Infante", Albox, Spain
Accepted by Scientific Culture for its vol. 2,
no. 1 (January 2016)
ABSTRACT
This article examines Oswald Spengler's claim that similarities
may be discerned in the style of mathematics, art and music developed by
a particular High Culture – looking first at his discussions of the Ancient
Greeks and how their thought-processes differed from that of Western Europeans,
as well as from the Persians and Arabs. An attempt is then made to extend
Spengler's theory to the Ancient Egyptians (referring to their Rhind Papyrus)
and to the Sino-Japanese (by appealing to their 'Sangaku' mathematical
art-forms). Finally, it is suggested that we may already be able to identify
certain distinctive features and characteristics of the recently born Russian
Culture.
KEYWORDS: Spengler, Comparative Mathematics,
Ancient Greece, Calculus, Ancient Egypt, Rhind Papyrus, Sangaku, Russia
INTRODUCTION
Immediately after the First World War, a German philosopher-historian
published a two-volumed book which evoked great interest and discussion
(Spengler, 1918 and 1922). After the 1940s, however, its popularity faded,
probably because it shared some common ground with Nazi ideals – although
Spengler (1933) criticized and was then disowned by them (Felken, 1988;
Farrenkopf, 2001; McNaughton, 2012).
Nevertheless, politics is not really the dominant theme in "The Decline
of the West". Spengler's principal thesis is that a culture or civilization
possesses its own distinctive soul, such that similar patterns may be discerned
in its 'creative expressions' in art, architecture, science, mathematics
and religion. For example, he argues that soaring Gothic cathedrals and
the characteristic style of Western music and painting, and the mathematical
tools which it developed, are all related to that culture's urge to explore
across distant horizons, as well as to its intense interest in the past
and concern for the far future (Spengler, 1918, pp. 174-178, 203, 183-184,
65). In a contrasting manner, the Ancient Greeks focussed primarily on
the corporeal and the 'here-now', such that sculpture was their favoured
art-form.
MATHEMATICS IN THE CLASSICAL (GRAECO-ROMAN) WORLD
For Greek mathematicians, number was "the essence of all things perceptible
to the senses" (Spengler, 1918, pp. 63-64) – usually involving the "measurement
of something near and corporeal". In order to ensure that these measurements
were well defined, they had to be represented by rational quantities
(i.e., which may be written as the quotient of two whole numbers). However,
when the Greeks tried to calculate the length of a diagonal in a square
or rectangle, they often encountered values like the square root of 2 –
which can never be expressed in terms of integers. Numbers like that are
termed irrational, and their discovery was regarded as "a secret
too dangerous to be revealed", such that a legend grew up claiming that
the man who had dared to publish this hidden mystery had perished by shipwreck
(Spengler, 1918, p.65).
What might be called their 'mental block' (which insisted that they
should work only with real, tangible values) helps to explain why there
was no zero in the Roman numeral-system; negative quantities were similarly
eschewed (Spengler, 1918, p.66).
Archimedes was extremely proud of his demonstration that the volume
of a sphere is 4pi/3 times the radius cubed, and asked for this formula
to be inscribed on his tombstone. According to one source, his proof involved
cutting the sphere up into thinner and thinner slices, and then computing
the volumes of the cylinders which would fit, as closely as possible, inside
and outside each slice. Another approach compared the respective masses
of a sphere, a cone and a cylinder.
Using integral calculus, on the other hand, the formula for the volume
of a sphere is derived in just a few lines.
WESTERN CULTURE
Differential and integral calculus emerged in Europe in the 17th century
as a totally new mathematical tool – discovered and devised simultaneously
by Newton and Leibniz. Its distinguishing feature lies in its ability to
deal with continuous rates of change (Spengler, 1918, p.126 note
3). This was a thought-process completely alien to Greek mathematicians
– a limitation which led to Zeno formulating his so-called paradox of the
race between Achilles and the tortoise.
Spengler (1918, pp. 230-231) insists that it was no accident that the
High Culture which gave birth to calculus, also created a music where "Melody
and embellishment join to produce the Motive, and this in development leads
to the rebirth of counterpoint in the form of the fugal style, of which
Frescobaldi was the first master and Bach the culmination".
West European mathematicians also conceived number-types which the Greeks
never even dreamed of, such as the square root of minus one (often represented
by 'i') – and the quantity written as 'e', termed "transcendental" because
it cannot be the root of any polynomial equation.
Thus, the identity
e^(i.pi) + 1 = 0
is widely considered to be one of the most beautiful 'jewels' in Western
mathematics: nobody ever regarded its discovery as "the sacrilegious revelation
of a forbidden secret".
THE ARAB-PERSIAN OUTLOOK COMPARED WITH OTHERS
Spengler (1918, p.382) describes the Arab-Persian Culture as one which
focussed on "the idea of substances with visible or secret attributes"
– thereby developing the science of Alchemy). He also points out
that the most striking features of Islamic architecture are found concealed
inside
the mosque (Spengler, 1918, pp. 184, 224).
He explains: "What we call Statics, Chemistry and Dynamics ... are really
the respective physical systems of the [Classical Greek, Arab-Persian and
Western] souls... Corresponding to these sciences, each to each, we have
the mathematics of Euclidean Geometry, Algebra, and Higher Analysis..."
(Spengler, 1918, p.384). He also compares each Culture's approach to painting
and art-work: "The Ancient Greeks ... recognised as actual only that which
was immediately present in time and place – and thus it repudiated the
background as pictorial element. The [Western one] strove through all sensuous
barriers towards infinity – and it projected the centre of gravity of the
pictorial idea into the distance by means of perspective. The [Persians
and Arabs] felt all happening as an expression of mysterious powers that
filled the world-cavern with their spiritual substance – and it shut off
the depicted scene with a gold background, that is, by something that stood
beyond and outside all nature-colours" (Spengler, 1918, pp. 247-248).
When discussing mathematics, Spengler (1918, pp. 71-73) emphasizes that
the 'algebra' which was developed by Al-Khwarizmi and others, involved
working with undefined magnitudes. Thus, their equations contained
unknowns 'x' and 'y' whose values had not yet been evaluated.
ANCIENT EGYPTIANS
The Rhind Papyrus gives an insight into some of the problems
addressed by ancient Egyptian mathematicians. In particular, they went
to the trouble of expressing fractions 2/n in the form of a series. For
example, they discovered that:
2/101 = 1/101 + 1/202 + 1/303 + 1/606.
The papyrus presents calculations of this sort for every such fraction
between 2/3 and 2/101 – i.e., covering all odd values of n.
For us, identities like that above are just a curiosity; we would probably
have remained unaware of them without the Rhind papyrus. But why did the
Egyptians regard them as significant and important?
It seems that they needed those expressions for dividing larger quantities;
e.g. the papyrus mentions that:
7/10 = 2/3 + 1/30, which then becomes 1/2 + 1/6 + 1/30 using the 2/n
table. For us, of course, this is a somewhat strange and clumsy way of
performing division.
Spengler (1918, pp. 188-189) depicts the Egyptian soul as one which
"saw itself moving down a narrow and inexorably prescribed life-path" ...
"The tomb temples of the Old Kingdom ... represent, not a purposed organization
of space such as we find in the mosque and the cathedral, but a rhythmically
ordered sequence of spaces ... that grow ever narrower and narrower".
JAPAN AND CHINA
"The [Chinese] temple is not a self-contained building, but a lay-out
– in which hills, water, trees, flowers and stones in definite forms and
dispositions are just as important as gates, walls, bridges and houses.
This Culture is the only one in which the art of gardening is a grand religious
art" (Spengler, 1918, p.190). "The Chinese park avoids energetic perspective.
It lays horizon behind horizon and, instead of pointing to a goal, tempts
to wander. The Chinese 'cathedral' of the early time, the Pi-Yung, [is
built around paths which wind] through gates and thickets, [and across]
stairs and bridges and courts" (Spengler, 1922, p.287). Here, it is illuminating
to compare chess with the Sino-Japanese game of GO – where the pieces do
not move around the board, but remain stationary after they have been placed
down. Despite that, GO is at least as subtle and difficult to master as
chess is.
Guided by the 'Tao' of life's path, the Chinese soul meanders through
its world (Spengler, 1918, pp. 203, 190, 310 note 2). It is probably no
coincidence that this High Culture discovered and developed the medical
technique of acupuncture.
Much of Japan's cultural heritage was derived from China. Nevertheless,
because of widespread destruction during the Mongol invasion, some aspects
of Chinese Culture (such as Tang dynasty architecture) are better preserved
in Japan. Earlier, many details of Chinese mathematical accomplishments
were lost when Shi-Hwang-Di carried out his infamous 'burning of the books'.
But Japanese geometry has shown us some very original 'theorems' – which
quite possibly would never have been discovered by Western mathematicians
– for example:
No matter how one triangulates a cyclic polygon, the sum of the inradii
of the triangles is constant; [Online: http://en.wikipedia.org/wiki/Japanese_theorem_for_cyclic_polygons
]
and:
Triangulating an arbitrary concyclic quadrilateral by its diagonals
yields four overlapping triangles (each diagonal creates two triangles)
– and the centres of the incircles of those triangles form a rectangle.
[Online: http://en.wikipedia.org/wiki/Japanese_theorem_for_cyclic_quadrilaterals
]
In Japan, it is customary to place wooden tablets (known as Sangaku)
as
offerings at Shinto shrines or Buddhist temples after engraving geometrical
problems on their surfaces. Many of these have been well illustrated and
mathematically analysed by Fukagawa and Rothman (2008; Rothman, 1988).
The three examples presented below, seem consistent with Spengler's description
of Sino-Japanese architecture and garden design. (Fukagawa and Rothman
supply answers to the first and third problems, but not to the second one).
It might be said that this manifestation of Japanese mathematics served
as an art-form – in addition to expressing religious devotion.
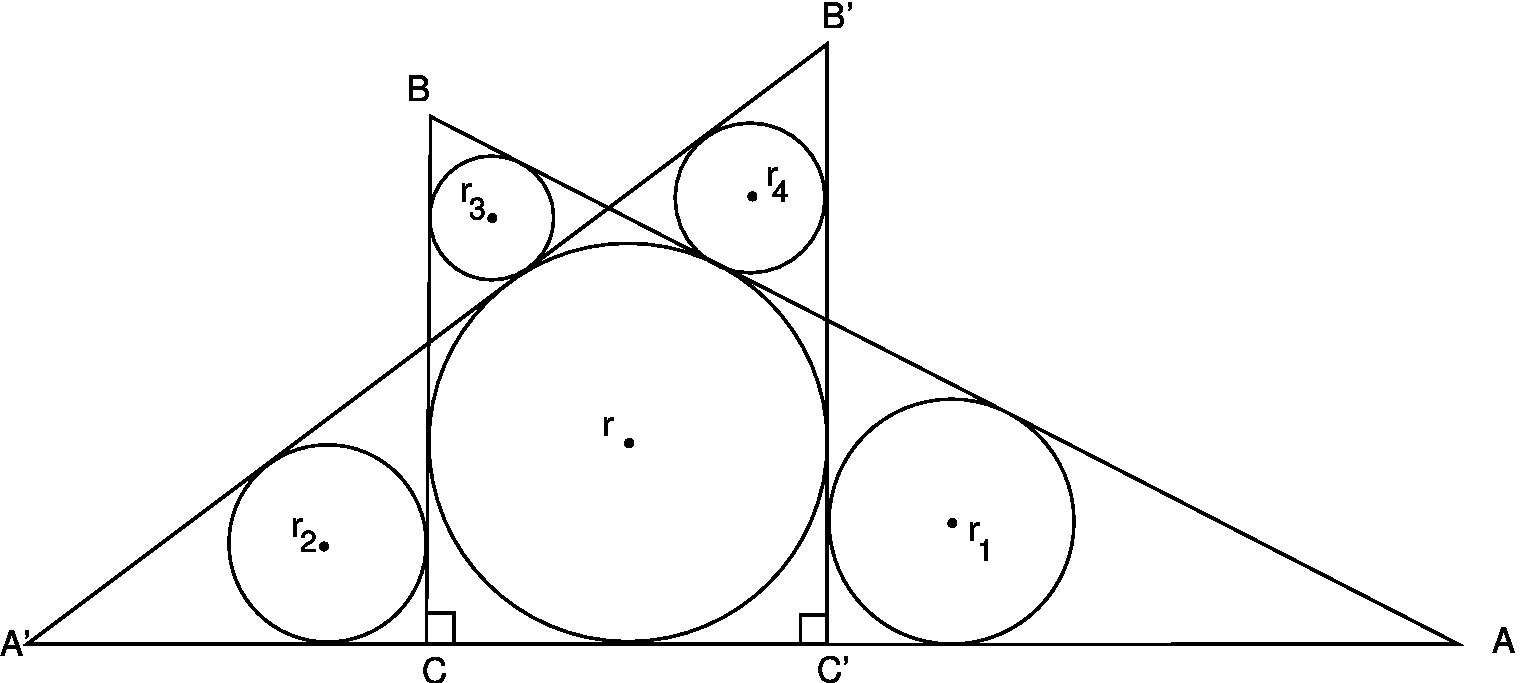
Problem 1. From Fukagawa and Rothman, p.158,
figure 5.17.
Two different-sized right-angled triangles are based on the same line.
The inscribed circle with radius r is common to both triangles.
Four other circles (with radii r1, r2, r3 and r4, all different) are
inscribed as shown. Prove that r1.r3 is always equal to r2.r4.
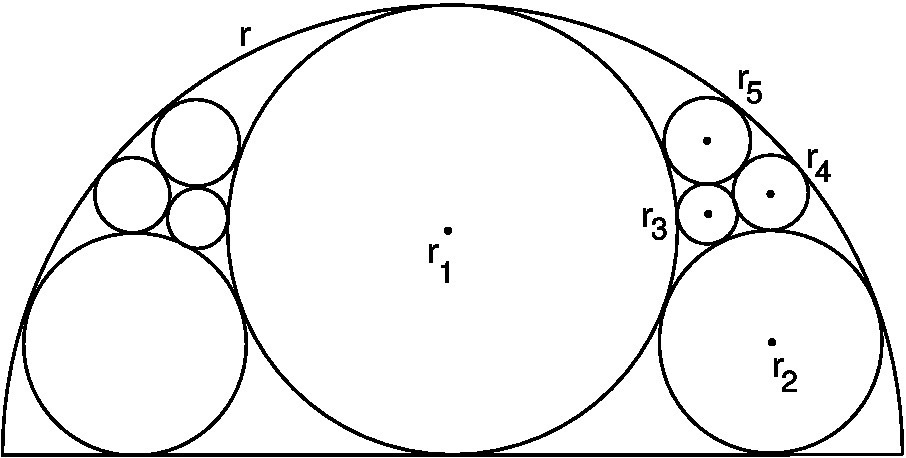
Problem 2. From Fukagawa and Rothman, p.335,
figure 10.23.
Nine circles fit inside a semicircle of radius r. The largest (i.e.,
central) circle has radius r1.
The diagram is symmetrical, so the four circles on the left have the
same radii as those on the right, that is r2, r3, r4 and r5.
Prove that r2 = r/4; r3 = r/15; r4 = r/12; r5 = r/10.
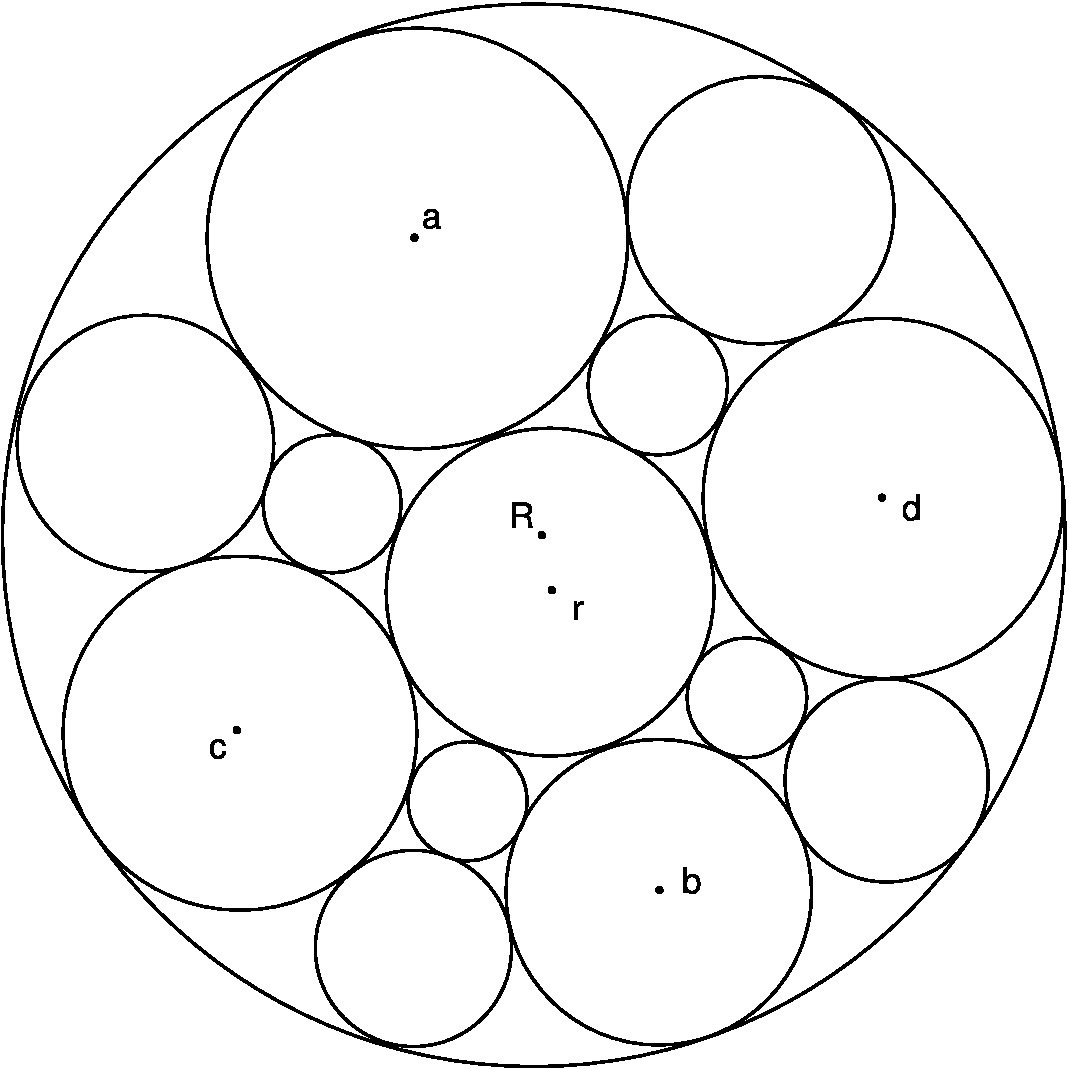
Problem 3. From Fukagawa and Rothman, p.200,
figure 6.11.
Thirteen circles, all of different sizes, fit exactly inside a larger
one whose radius is R. Four of them have radii of length a, b, c and d,
as shown.
Prove that the following relation always holds: 1/a + 1/b = 1/c + 1/d
RUSSIA AND THE FUTURE
Spengler (1922, pp. 192-196, and 1934) believes that a new High Culture
has recently crystallized in Russia. He even attempted to discern and analyse
the nature and character of its 'soul'. For example, he maintained that
the Russian death-impulse "is an expressing and expanding of self (Sichentäussern)
till 'it' in the man becomes identical with the boundless plain itself...
That 'All are responsible for all' ... is the metaphysical fundament
of all Dostoyevski's creation. Mystical Russian love is the love of brothers
under equal pressure all along the earth., ever along and along" (Spengler,
1922, p.295 note 1).
Spengler may not be completely correct in asserting that the 'prime
symbol' of the new Russian Culture is the infinite plain. If so,
he can perhaps be forgiven – because he made that assessment one hundred
years ago. But if he is right that another 'Cultural organism' has indeed
been born, then new discoveries and developments in mathematics, art and
music will blossom there. On that assumption, can we try and guess what
sort of mathematics might emerge?
Without doubt, Russian mathematicians have already made prominent contributions
in that field. In particular, Grigori Perelman should be highlighted for
demonstrating the truth of the Poincaré Conjecture. In 2006,
the world-renowned journal “Science” recognized his achievement as the
scientific ‘Breakthrough of the Year’ – the first time such a tribute had
ever been accorded in mathematics (Mackenzie, 2006). For his work, Perelman
was also awarded the highly prestigious Fields Medal – but refused
it. After interviewing him, John Ball (outgoing president of the International
Mathematical Union) remarked: "He has a different psychological make-up,
which causes him to see life differently" (BBC News, 2006).
Earlier, Perelman had confirmed the Soul Conjecture with (what
Wikipedia describes as) "an astonishingly concise proof". His two discoveries
are important insights and landmarks in the development of mathematical
topology (which may be defined as the study of spaces and their
connectivity). So perhaps the new Russian mathematics will specialise
in this topic? For example, eventually it might produce a comparatively
simple proof of the Four Colour Theorem (explained by Appel and
Haken, 1977).
If the Spenglerian 'timetable' is correct, Russian art, music and mathematics
will attain their zenith (after a few more centuries) during what he calls
their 'summertime' – so it is probably too soon to know how exactly they
will manifest themselves. Despite that, it is worth asking whether the
Russian ability and love for the [Western] game of Chess is evidence
that a new cultural soul is unfolding in that landscape. Each piece on
the chessboard commands or controls only certain squares, i.e. a 'subspace'
of the whole. And game-strategy assesses how the power or potential of
each piece can best coordinate and interact with the others.
In a different field, there might be grounds for arguing that it was
no coincidence that the Periodic Table of the Elements was first
conceived in a Russian mind – that of Dmitri Mendeleyev – rather than a
Western one.
ACKNOWLEDGEMENT
Tony Rothman very kindly supplied the diagrams for Problems 1, 2 and
3.
REFERENCES
APPEL, K. and HAKEN, W. (October 1977). "Solution of the Four Color
Map Problem". Scientific American, Vol. 237, No. 4,
108–121.
BBC NEWS, SCIENCE/NATURE (22 August 2006). "Maths genius declines top
prize".
Online: http://news.bbc.co.uk/2/hi/science/nature/5274040.stm
FARRENKOPF, J. (2001). "Prophet of Decline: Spengler on World History
and Politics", p.236. Baton Rouge: Louisiana State University Press.
FELKEN, D. (1988). "Oswald Spengler: Konservativer Denker zwischen Kaiserreich
und Diktatur", pp. 194-198 and 217-223. Munich: C.H. Beck.
FUKAGAWA, H. and ROTHMAN, T. (2008). "Sacred Mathematics – Japanese
Temple Geometry". Oxford: Princeton University Press. Accessible:
kknop.com/math/sangaku.pdf
MacKENZIE, D. (December 2006). "Breakthrough of the year: The Poincaré
Conjecture—proved". Science, Vol. 314, No. 5807, 1848–1849.
Online:http://www.sciencemag.org/content/314/5807/1848.full
McNAUGHTON, D.L. (2012). "Spengler's philosophy, and its implication
that Europe has 'lost its way'". Comparative Civilizations Review,
Vol. 67, 7-15. Online: http://www.dlmcn.com/oswaldspengler.html
ROTHMAN, T. (May 1998). "Japanese Temple Geometry". Scientific American,
Vol. 278, No. 5, 84-91.
SPENGLER, O. (1918). "The Decline of the West", Vol. I.
London: George Allen & Unwin. (Original German title: "Der Untergang
des Abendlandes").
Online: https://archive.org/stream/Decline-Of-The-West-Oswald-Spengler/Decline_Of_The_West
SPENGLER, O. (1922). "The Decline of the West", Vol. II.
London: George Allen & Unwin. Online: https://archive.org/stream/Decline-Of-The-West-Oswald-Spengler/Decline_Of_The_West#page/n661/mode/2up
SPENGLER, O. (1933). "The Hour of Decision", pp. xiv et seq., xii, 7.
New York: Alfred A. Knopf. (Original German title: "Jahre der Entscheidung").
SPENGLER, O. (1934). "Politische Schriften", pp. 122, 136-137. Munich:
C.H. Beck.
= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =
= = = = = = = = = = = = = = = = = = = = = = =
Author’s website:
http://DLMcN.com
E-mail: DLMcN@yahoo.com
Correspondence on Spengler:
http://DLMcN.com/histcorr.html
Mathematics page:
http://DLMcN.com/page5.html